数据结构（五）二叉搜索树

小艾

数据结构

发布于：Jun 8, 2022

1.5k words

5 min

树的概念

之前介绍的所有的数据结构都是线性存储结构。本章所介绍的树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。

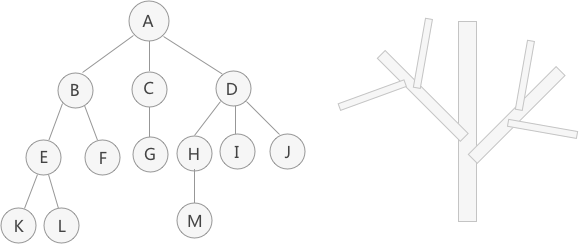
图 1(A) 是使用树结构存储的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意图。对于数据 A 来说，和数据 B、C、D 有关系；对于数据 B 来说，和 E、F 有关系。这就是“一对多”的关系。

将具有“一对多”关系的集合中的数据元素按照图 1（A）的形式进行存储，整个存储形状在逻辑结构上看，类似于实际生活中倒着的树（图 1（B）倒过来），所以称这种存储结构为“树型”存储结构。

树的结点

结点：使用树结构存储的每一个数据元素都被称为“结点”。例如，图 1（A）中，数据元素 A 就是一个结点；

父结点（双亲结点）、子结点和兄弟结点：对于图 1（A）中的结点 A、B、C、D 来说，A 是 B、C、D 结点的父结点（也称为“双亲结点”），而 B、C、D 都是 A 结点的子结点（也称“孩子结点”）。对于 B、C、D 来说，它们都有相同的父结点，所以它们互为兄弟结点。
树根结点（简称“根结点”）：每一个非空树都有且只有一个被称为根的结点。图 1（A）中，结点 A 就是整棵树的根结点。
叶子结点：如果结点没有任何子结点，那么此结点称为叶子结点（叶结点）。例如图 1（A）中，结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。

树根的判断依据为：如果一个结点没有父结点，那么这个结点就是整棵树的根结点。

子树和空树

子树：如图 1（A）中，整棵树的根结点为结点 A，而如果单看结点 B、E、F、K、L 组成的部分来说，也是棵树，而且节点 B 为这棵树的根结点。所以称 B、E、F、K、L 这几个结点组成的树为整棵树的子树；同样，结点 E、K、L 构成的也是一棵子树，根结点为 E。

注意：单个结点也是一棵树，只不过根结点就是它本身。图 1（A）中，结点 K、L、F 等都是树，且都是整棵树的子树。

知道了子树的概念后，树也可以这样定义：树是由根结点和若干棵子树构成的。

空树：如果集合本身为空，那么构成的树就被称为空树。空树中没有结点。

补充：在树结构中，对于具有同一个根结点的各个子树，相互之间不能有交集。例如，图 1（A）中，除了根结点 A，其余元素又各自构成了三个子树，根结点分别为 B、C、D，这三个子树相互之间没有相同的结点。如果有，就破坏了树的结构，不能算做是一棵树。

有序树和无序树

如果树中结点的子树从左到右看，谁在左边，谁在右边，是有规定的，这棵树称为有序树；反之称为无序树。

在有序树中，一个结点最左边的子树称为”第一个孩子”，最右边的称为”最后一个孩子”。

拿图 1（A）来说，如果是其本身是一棵有序树，则以结点 B 为根结点的子树为整棵树的第一个孩子，以结点
D 为根结点的子树为整棵树的最后一个孩子。

二叉树的定义

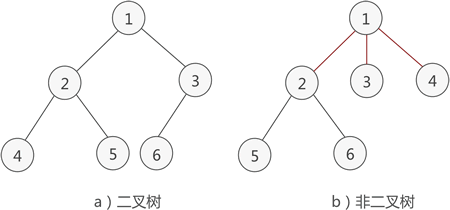
简单地理解，满足以下两个条件的树就是二叉树：

本身是有序树；
树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2；

二叉搜索树（又叫做二叉查找树或二叉排序树）具备以下特点：

每个结点的值均大于其左子树上的任意一个结点的值
每个结点的值均小于其右子树上任意一个结点的值

二叉搜索树的基本操作：

BSTNode* BST_Search(BSTree T, int key);：查找关键字 (非递归版本)
BSTNode* BST_SearchR(BSTree T, int key);：查找关键字 (递归版本)
bool BST_Insert(BSTree &T, int key);：二叉排序树插入操作
void BST_Create(BSTree &T, int *elems, int n);：构造二叉排序树

二叉搜索树的实现

/**
 * 二叉排序树
 */
typedef struct BSTNode{
    int data;
    struct BSTNode *lchild, *rchild;
} BSTNode, *BSTree;

/**
 * 二叉排序树的插入操作
 *
 * @param T
 * @param i
 * @return
 */
bool BST_Insert(BSTree &T, int key){
    // 首先判断是否是树根
    if (NULL == T) {
        // 为新节点申请空间
        T = (BSTree)malloc(sizeof(BSTNode));
        T->data = key;
        T->lchild = T->rchild = NULL;
    } else if (key == T->data) {
        // 发现相同元素
        return false;
    } else if (key < T->data) {
        // 如果要插入的结点，小于当前结点，将插入左子树
        return BST_Insert(T->lchild, key);
    } else {
        // 如果要插入的结点，大于当前结点，则插入右子树
        return BST_Insert(T->rchild, key);
    }
};

/**
 * 构造二叉排序树
 *
 * @param T
 * @param elems
 * @param n
 */
void BST_Create(BSTree &T, int elems[], int n){
    int i = 0;
    while (i < n) {
        BST_Insert(T, elems[i]);
        i++;
    }
};

/**
 * 非递归搜索子树
 *
 * @param T
 * @param key
 * @param p
 * @return
 */
BSTree BST_Search(BSTree T, int key) {
    while (T != NULL && T->data != key) {
        if (T->data < key) {
            // 如果 key 大于当前结点则返回右子树
            T = T->rchild;
        } else {
            // 如果 key 小于当前结点则返回左子树
            T = T->lchild;
        }
    }
    return T;
};

/**
 * 递归搜索子树
 *
 * @param T
 * @param key
 * @return
 */
BSTree BST_SearchR(BSTree T, int key){
    if (T != NULL && T->data != key) {
        if (T->data < key) {
            return BST_SearchR(T->rchild, key);
        } else if (T->data > key) {
            return BST_SearchR(T->lchild, key);
        }
    }
    return T;
};